
you spin me…
The ciphertext is just encrypted with a rotation cipher. I decrypted it with the tool at https://www.dcode.fr/rot-cipher. The plaintext is SOC_CTF{LIKE_A_RECORD}
Water Affinity
From the title we can guess that the text is encrypted with the affine cipher. So we can plug it into this tool https://www.dcode.fr/affine-cipher. The plain text is SOC_CTF{DUCKS_LOVE_WATER}.
One More Time
So with this one, it looks like we are given a key along with the ciphertext (CT). Given the title of the problem, a cipher to try is a one-time pad. After trying that and having it not work we could try the Vigenere Cipher. It could operate as a one-time pad as long as the input string is long enough. So we’ll try entering the key and CT at this website to decode it https://www.dcode.fr/vigenere-cipher. After putting in the key and CT we can decrypt it to get this plaintext: ducksaregonnacelebrate. From here we can add on the flag markers to get our solution: SOC_CTF{ducksaregonnacelebrate}.
9.8m/s sinks
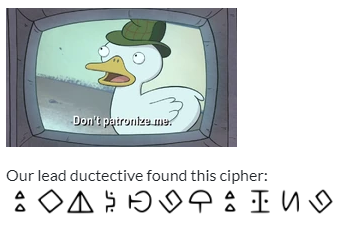
You can do a reverse image search on this to find that the image is from a show called Gravity Falls. From here you can look up ciphers that are used in the show. From the look of the symbols, It was the Bil Cipher(Symbol chart here https://www.dcode.fr/gravity-falls-bill-cipher) . So we can manually just go through and decrypt this to get the cipher text: SOC_CTF{TWINBROTHER}.
I’m not a witch, I’m your duck!
For this challenge, your supposed to use the poem to determine the encryption method. The method essentially works like this. Grab the alphabet in order. Take every other letter and split them into two lists. From here grab each letter from the Cipher Text (CT) and find where it is in a list. And from there swap it with a letter that matches the corresponding position in the other list. Here is my code for doing this quickly:
l1 = ["a","c","e","g","i","k","m","o","q","s","u","w","y"]
l2 = ["b","d","f","h","j","l","n","p","r","t","v","x","z"]
text = "GFKKPNZMBNFJTJMJHPNBKKBQCZPVLJKKFCNZEBSGFQOQFOBQFSPCJF"
text = text.lower()
output = ""
for i in text:
found = False
for j in range(len(l1)):
if i == l1[j]:
found = True
output += l2[j]
if not found:
for j in range(len(l2)):
if i == l2[j]:
found = True
output += l1[j]
print(output.upper())
If we run this code we get our flag text out of it which is HELLOMYNAMEISINIGOMALLARDYOUKILLEDMYFATHERPREPARETODIE. From here we wrap it in the flag markers for our final solution: SOC_CTF{HELLOMYNAMEISINIGOMALLARDYOUKILLEDMYFATHERPREPARETODIE}.
Secrets
For this challenge, we received this text file. In this, we see a list of tuples that list 1 through 5 and then some other numbers on the right. Then we have n=5 and k=3. It seems we are using Shamir secret sharing to encrypt the flag. And it seems that each letter is individually encrypted. So we will need to step through each one to get the letter back out of it. Here is my code for decrypting each letter once we read it from the file:
# Reconstruct the secret from shares using Lagrange interpolation (simplified version)
def reconstruct_secret(shares, k):
# Simplified Lagrange interpolation for demonstration purposes
def lagrange_interpolate(x, x_s, y_s):
sum = 0
for i in range(k):
xi, yi = x_s[i], y_s[i]
prod = 1
for j in range(k):
if i == j:
continue
xj = x_s[j]
prod *= (x - xj) / float(xi - xj)
sum += yi * prod
return sum
x_s, y_s = zip(*shares)
return lagrange_interpolate(0, x_s, y_s)
reconstruction = ""
# This assumes secrets looks like this [[(x,y),(x,y),(x,y)], etc... ]
for i in secrets:
r = reconstruct_secret(i[:3], 3)
reconstruction += chr(int(r))
print("reconstruction: " + reconstruction)
Once you get done decrypting all the shares you should get this as the output text: SOC_CTF{D@rk_Wing_H@s_M@d_skills}.
